LRU和LFU算法
LRU算法
简介
LRU (Least Recently Used) 算法即最近最久未使用,每次选择最近最久未使用的页面淘汰掉。
实现过程
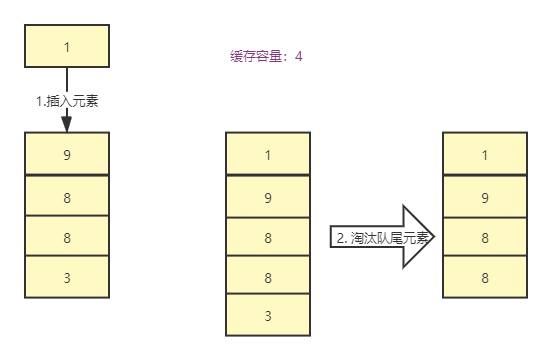
- 新增数据时,元素插入到队列头部。
- 访问元素(查询、更新和删除)时,将元素移动到队列头部。
- 当超过内存限制,需要淘汰数据时,将已排序队列的最后元素删除。
数据结构
LRU 算法内部的数据结构需要根据元素的访问时间排序。还需要查找、插入、删除等效率要高。
- 查找、插入、删除快。
- 支持排序。
在常用的集合中,有的是查找更新快或者插入删除快,没有数据结构能同时满足以上条件,所以需要采用组合的数据结构。
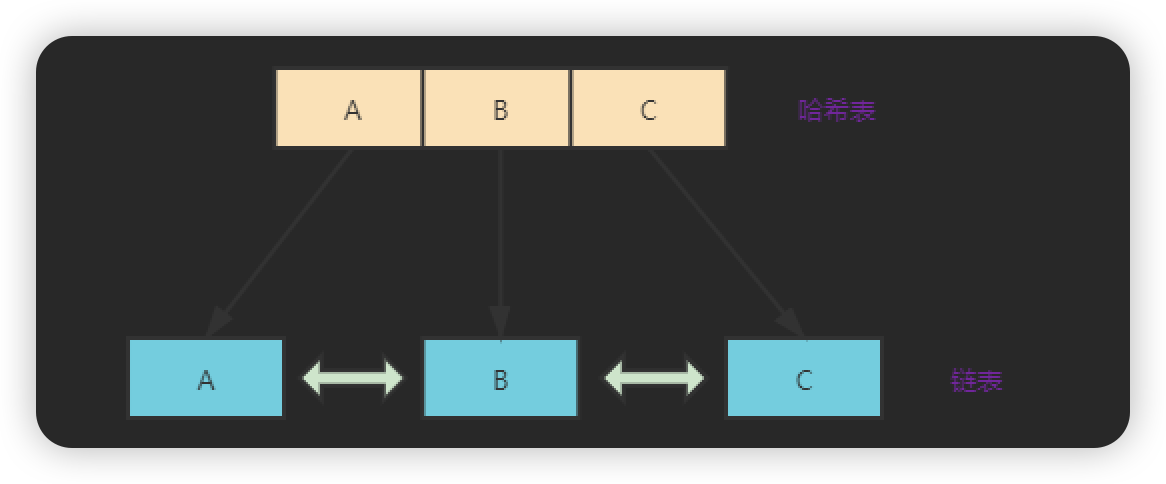
在 LRU 算法中,使用的是哈希链表的数据结构,来同时保证查找、插入、删除的速度,同时链表还能够满足排序。
LinkedHashMap
LinkedHashMap 底层数据结构是哈希链表,是 HashMap + DoubleLinkedList,其中 HashMap 用来存放数据,而 DoubleLinkedList 用来维护插入元素的先后顺序。
在 LinkedHashMap 中有一个方法 removeEldestEntry 是支持 LRU 算法的。
protected boolean removeEldestEntry(Map.Entry<K,V> eldest) {
//默认为false
return false;
}当方法 removeEldestEntry 返回 true 的时候,会删除集合内最旧的元素。在每次新增元素调用 put 或 putAll 方法时,新增完元素之后调用该方法,以此来减少内存消耗。
public class LruCacheDemo<K,V> extends LinkedHashMap<K,V> {
//容量
private int capacity;
public LruCacheDemo(int capacity){
//accessOrder:访问顺序(true,内部元素会按照访问顺序重新排列;false:内部元素不会按照访问顺序重新排列)
//符合 LRU 算法时,新访问的数据要重新排列到队尾,以免提前出队。
super(capacity,0.75F,false);
this.capacity=capacity;
}
@Override
protected boolean removeEldestEntry(Map.Entry<K, V> eldest) {
//重写该方法,当集合容量>预设容量时,删除最近最久未使用的元素,这也是实现 LRU 算法的关键。
return super.size()>capacity;
}
}其中,LinkedHashMap 的构造函数中有一个参数为 accessOrder,代表集合内部元素是否根据访问顺序重新排列。
以下面测试例子为例来区分 accessOrder 参数的作用。
public static void main(String[] args) {
LruCacheDemo<Integer,Integer> lruCacheDemo = new LruCacheDemo<Integer,Integer>(3);
lruCacheDemo.put(1,1);
lruCacheDemo.put(2,2);
lruCacheDemo.put(3,3);
System.out.println(lruCacheDemo.keySet());
lruCacheDemo.put(4,4);
System.out.println(lruCacheDemo.keySet());
lruCacheDemo.put(3,3);
lruCacheDemo.put(3,3);
lruCacheDemo.put(3,3);
System.out.println(lruCacheDemo.keySet());
lruCacheDemo.put(5,5);
System.out.println(lruCacheDemo.keySet());
}accessOrder = true;
内部元素根据访问顺序会重新排列,访问的元素排列到队尾。
java//output [1, 2, 3] [2, 3, 4] [2, 4, 3] [4, 3, 5]accessOrder = false;
内部元素不会根据访问顺序重新排列,按照插入的顺序进行排列。
java//output [1, 2, 3] [2, 3, 4] [2, 3, 4] [3, 4, 5]
手写LRU算法
前面分析了 LRU 算法的核心就是底层数据结构要使用哈希链表,哈希表我们可以使用 HashMap,而链表需要我们来手写一个链表(单向双向都可以,这里实现的是双向链表)。
除了实现链表本身具有的有序性外,还由于 LRU 算法要求访问过的数据放到队尾,所以必须包含以下方法。
添加元素到队尾。
每次新增都插入到队尾的位置(访问、更新元素时也要放到队尾)。
获取头结点元素。
在内部缓存满的时候,删除最近最久未使用元素。
删除元素。
Node类
实现的是双向链表,包含一个前驱和一个后继。
/**
* 结点类
*/
class Node<K, V> {
K key;
V value;
//前驱
Node<K, V> prev;
//后继
Node<K, V> next;
public Node() {
//初始化时,前驱和后继都是null
this.prev = this.next = null;
}
public Node(K key, V value) {
this.key = key;
this.value = value;
//初始化时,前驱和后继都是null
this.prev = this.next = null;
}
}双向链表
实现的双向链表,包含头尾指针,还实现了添加元素到尾部、删除结点、获取第一个节点等方法。
/**
* 双向链表
*/
class DoubleLinkedList<K, V> {
Node<K, V> head;
Node<K, V> tail;
public DoubleLinkedList() {
//头尾节点都为空
head = new Node<>();
tail = new Node<>();
head.next = tail;
tail.prev = head;
}
//添加到尾部
public void addTail(Node<K, V> node) {
node.next=tail;
node.prev= tail.prev;
tail.prev.next = node;
tail.prev= node;
}
//删除结点
public void remove(Node<K, V> node) {
node.next.prev = node.prev;
node.prev.next = node.next;
node.prev = null;
node.next = null;
}
//获取第一个结点
public Node<K, V> getHead() {
return head.next;
}
}LRU算法实现类
以 HashMap 来保存结点数据,用手写的双向链表来保存元素的访问顺序。
public class LruCacheDemo {
private int cacheSize;
//哈希表,保存元素内容
private Map<Integer, Node<Integer, Integer>> map;
//双向链表,保存元素顺序
private DoubleLinkedList<Integer, Integer> doubleLinkedList;
public LruCacheDemo(int cacheSize){
this.cacheSize=cacheSize;
this.map=new HashMap<>();
doubleLinkedList=new DoubleLinkedList<>();
}
public int get(Integer key) {
//不存在
if (!map.containsKey(key)) {
return -1;
}
Node<Integer, Integer> node = map.get(key);
//调整访问节点的位置
doubleLinkedList.remove(node);
doubleLinkedList.addTail(node);
return node.value;
}
public void put(Integer key, Integer value) {
if(map.containsKey(key)){
Node<Integer, Integer> oldNode = map.get(key);
oldNode.value=value;
//调整更新元素的位置
doubleLinkedList.remove(oldNode);
doubleLinkedList.addTail(oldNode);
return;
}
if(map.size()>=cacheSize){
//缓存已满,淘汰最近最久未使用的元素
Node<Integer, Integer> tailNode = doubleLinkedList.getHead();
map.remove(tailNode.key);
doubleLinkedList.remove(tailNode);
}
//新插入元素
Node<Integer,Integer> newNode = new Node<>(key,value);
map.put(key,newNode);
doubleLinkedList.addTail(newNode);
}
//获取排序key列表
private List<Integer> sortKeyList(){
List<Integer> list = Lists.newArrayList();
//获取第一个结点
Node<Integer, Integer> node = doubleLinkedList.head.next;
while (node.next!=null){
//匹配到尾指针,结束
if(node==doubleLinkedList.tail){
break;
}
list.add(node.value);
//遍历下一个结点
node=node.next;
}
return list;
}
public static void main(String[] args) {
LruCacheDemo lruCacheDemo = new LruCacheDemo(3);
lruCacheDemo.put(1,1);
lruCacheDemo.put(2,2);
lruCacheDemo.put(3,3);
System.out.println(lruCacheDemo.sortKeyList());
lruCacheDemo.put(4,4);
System.out.println(lruCacheDemo.sortKeyList());
lruCacheDemo.put(3,3);
lruCacheDemo.put(3,3);
lruCacheDemo.put(3,3);
System.out.println(lruCacheDemo.sortKeyList());
lruCacheDemo.put(5,5);
System.out.println(lruCacheDemo.sortKeyList());
}
}
//output
[1, 2, 3]
[2, 3, 4]
[2, 4, 3]
[4, 3, 5]LRU算法的缺陷
在 LRU 算法中,当热点数据比较多的时候,淘汰时能够把冷数据给淘汰点。但是当某些冷数据被突然访问的时候,根据 LRU 的策略,很可能把热点数据淘汰掉,这种情况下,存在缓存污染的问题。

LFU算法
简介
LFU (Least Frequently Used) 算法为最不经常使用,每次将使用次数最少的页面给淘汰掉。
LFU 算法基于如果一个数据在最近一段时间内使用次数很少,那么在将来一段时间内被使用的可能性也很小的考虑出发来实现。
实现过程
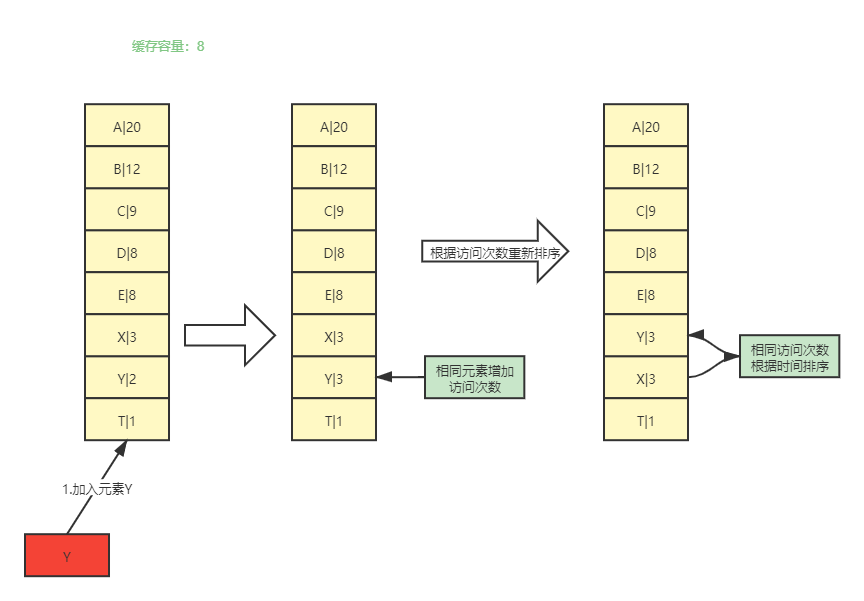
- 新增数据时,元素插入到队列尾部,元素访问次数加 1。
- 访问元素(查询、更新和删除)时,元素访问次数加 1,队列需要重新排列。
- 若元素访问次数相同,则根据元素的访问时间进行排序。
- 当超过内存限制,需要淘汰数据时,将已排序队列的最后元素删除。
LFU和 LRU 比较
- LFU 能够避免 LRU 的缺陷,即某些冷数据突然被访问导致热点数据被淘汰的问题,又称缓存污染。但是 LFU 同样也具有问题。
- LFU 需要记录数据的历史访问记录,若 LRU 中的热点数据由于访问模式的修改变为冷数据,意味着之前的热点数据在接下来很长时间不会被访问,但是由于之前的访问计数器的缘故,转换后的冷数据在很长时间都不会被删除。即 LFU 中的历史数据会占用缓存,同样存在缓存污染问题。
- LFU 算法需要记录所有数据的访问记录,消耗内存。
- LFU 算法元素每次修改后,都需要对队列重排序,性能消耗较高。