常用数据结构
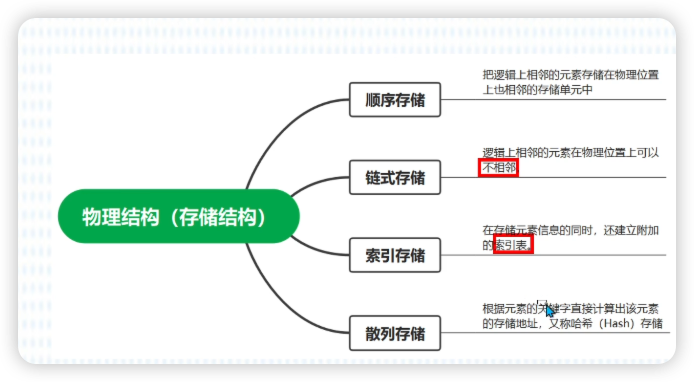
存储结构
复杂度
时间复杂度
空间复杂度
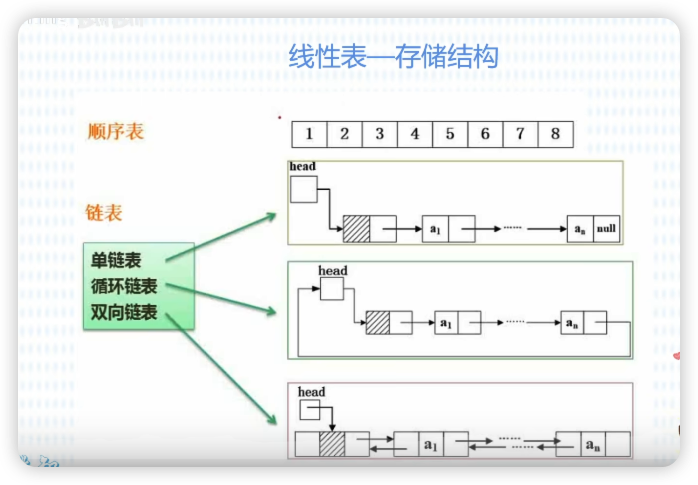
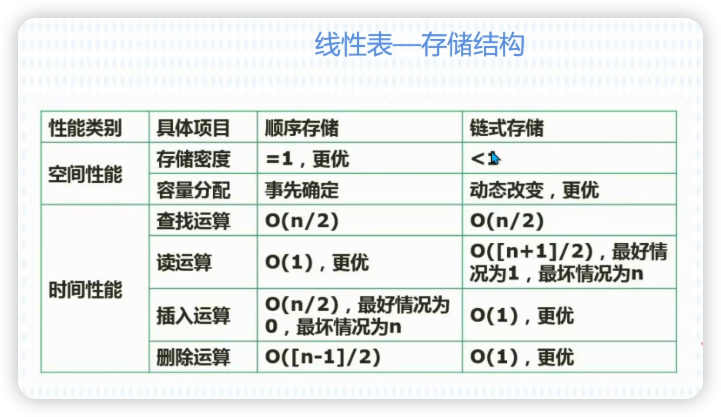
线性表
串
比如字符串。

数组

矩阵

求矩阵元素下标,直接代入即可。

代入 A(0,0) 和 A(0,1),分别对应 M(1) 和 M(2)。
因为 M[1..m] 是从 1 开始的。
广义表

例1:长度为3,深度为2
例2: 先取表尾,再取表头,再取表头。
head (head ( tail(LS1) ) )
广义表的基本运算
- 取表头
- 取表尾
二叉树
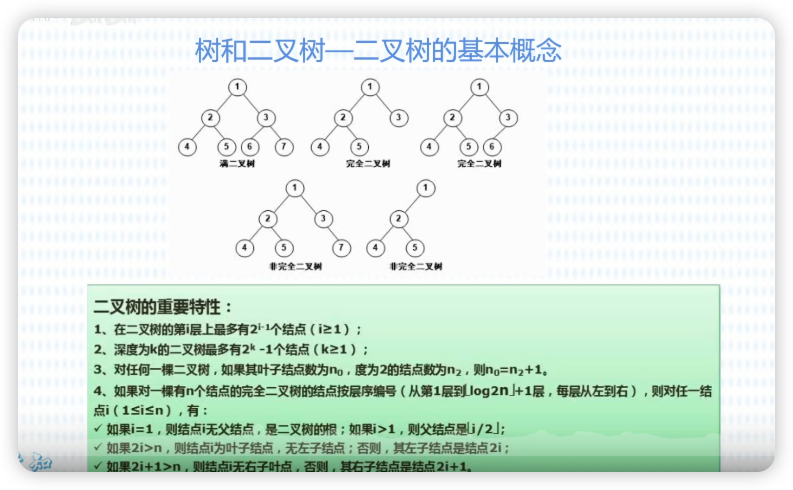
满二叉树
节点度都为2。
完全二叉树
节点保持有序。
特性
- 任何一颗二叉树,如果叶子结点为n0,度为 2 的节点为 n,则 n0=n2+1。
遍历
- 前序遍历:根左右(^ ← →)
- 中序遍历:左根右 (← ^ →)
- 后序遍历:左右根 (← → ^)
左右顺序是不变的,根的位置依次在1、2、3的位置上。
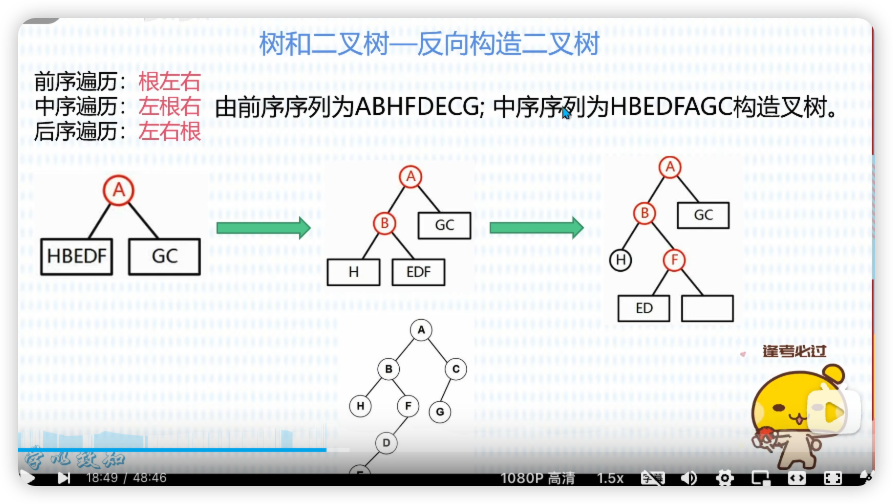
反向构造二叉树
根据前序遍历规则,第一个元素为根元素,找到根元素。
一步一步拆解,左子树右子树。
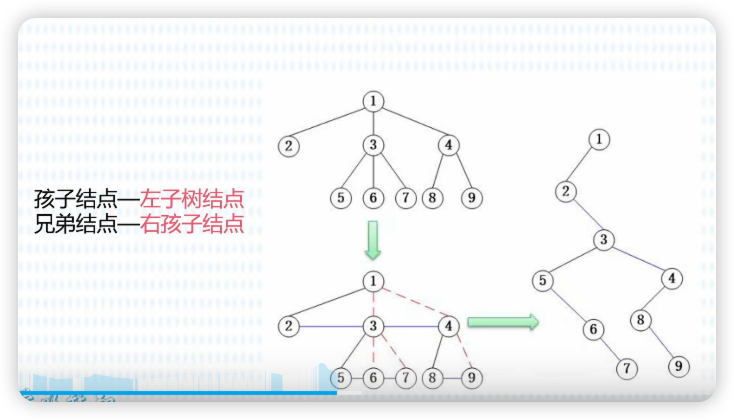
树转二叉树
满足两个规则,即刻画出二叉树。
- 孩子节点 - 放到左子树
- 兄弟节点 - 放到右子树
二叉排序树
满足两个规则即可:
- 左孩子小于根
- 右孩子大于根

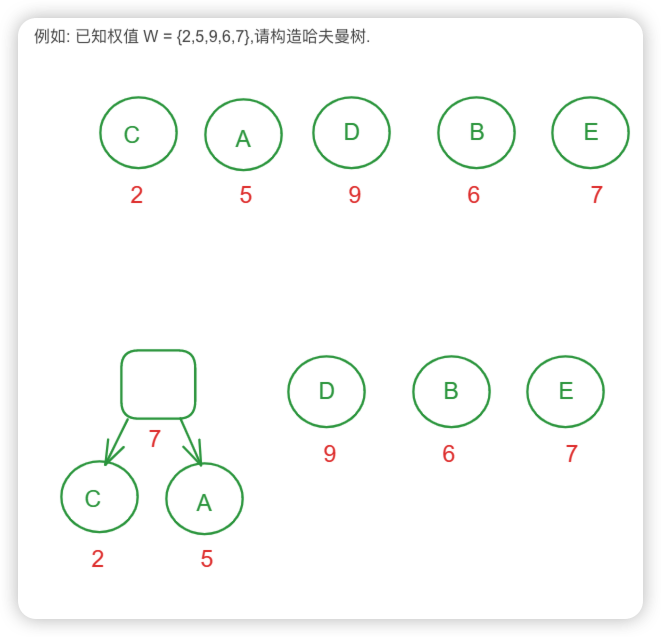
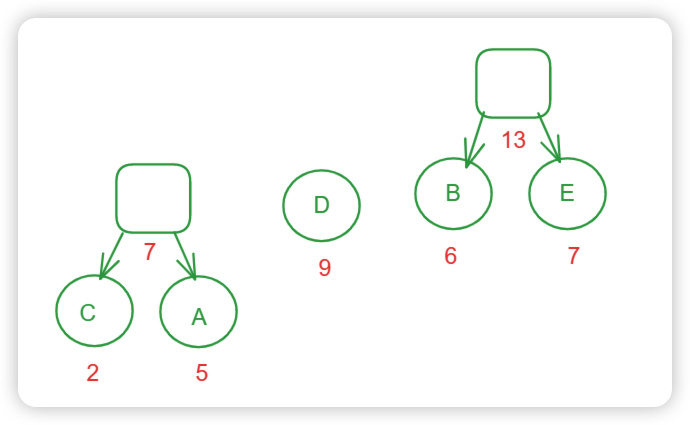
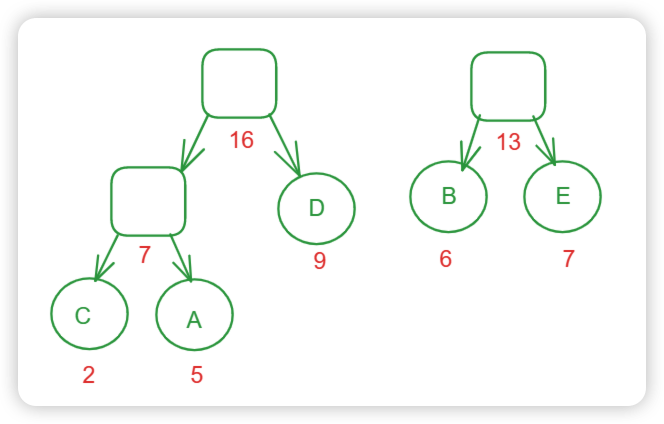
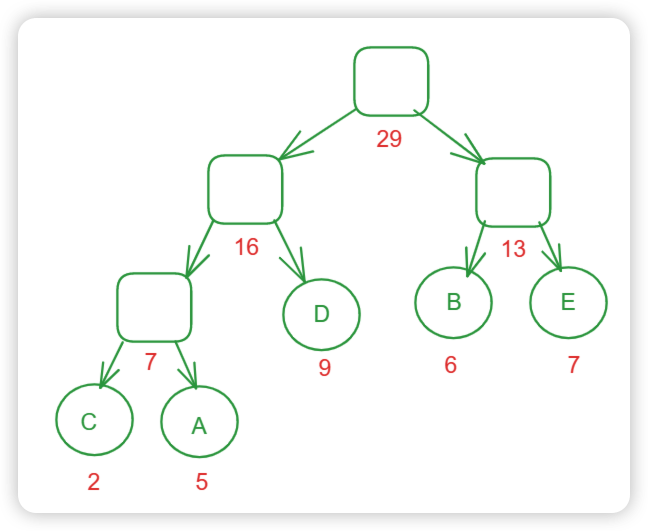
哈夫曼树-最优二叉树
哈夫曼树 是一种最优树, 是一类带权路径长度最短的二叉树。
构建哈夫曼树的核心就是选出来最小的两个节点去构造。
两个节点相加的值作为新元素进行比较。
线索二叉树
线索二叉树优化了二叉树遍历和查找效率的数据结构。在叶子或者度为1 的节点增加指针。
- 某个节点只有一个子节点。
- 叶子结点没有子节点。
这些节点的左右子树空间未利用起来。加速后续查找的速度。
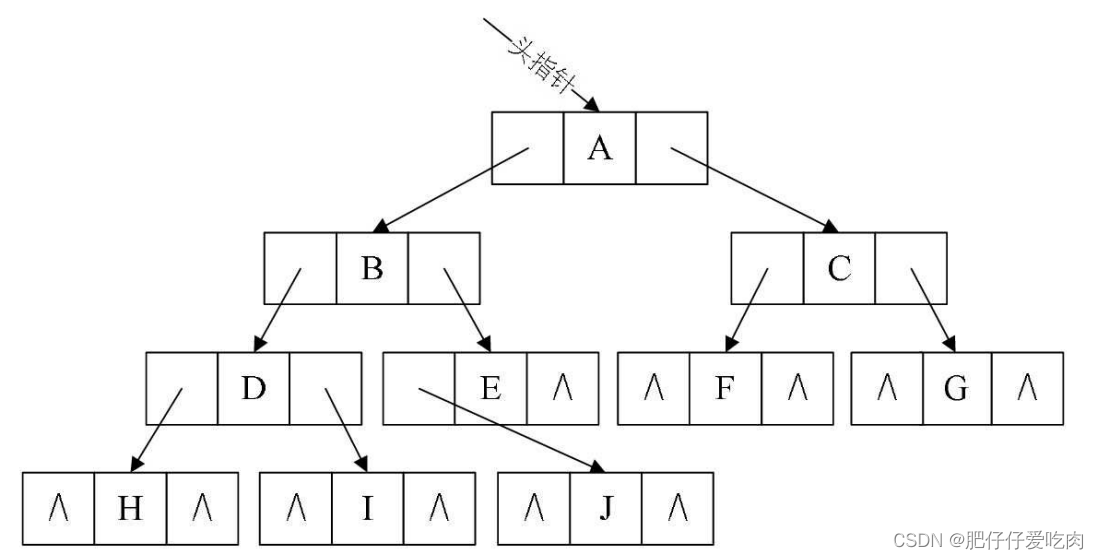
无论是前序遍历,中序遍历还是后序遍历。
- 如果一个节点没有左子节点就让他的左指针指向他的前驱节点。
- 如果一个节点没有后继节点,就让他的右指针指向他的后继节点。
中序遍历线索化
比如下面这棵树
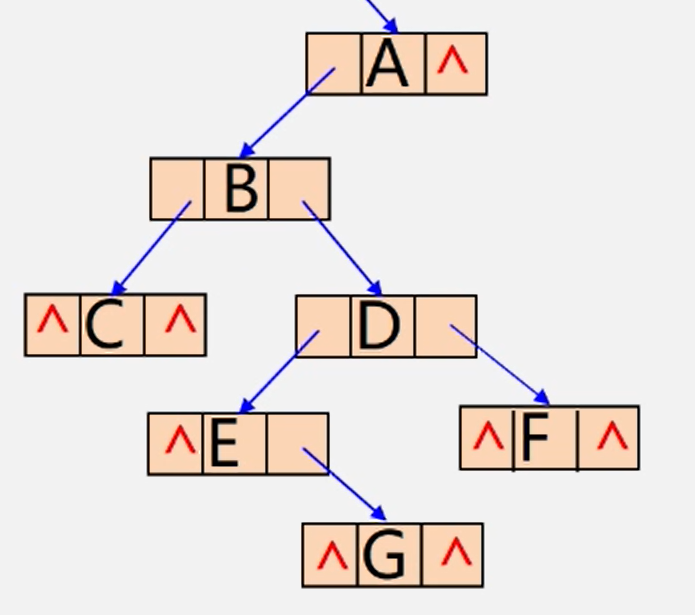
首先采用左根右的方式遍历,得到 CBEGDFA。
然后按照中序遍历,设置线索。
- 比如C左指针为空,右指针指向B。
- 比如G左指针指向E,右指针指向D。
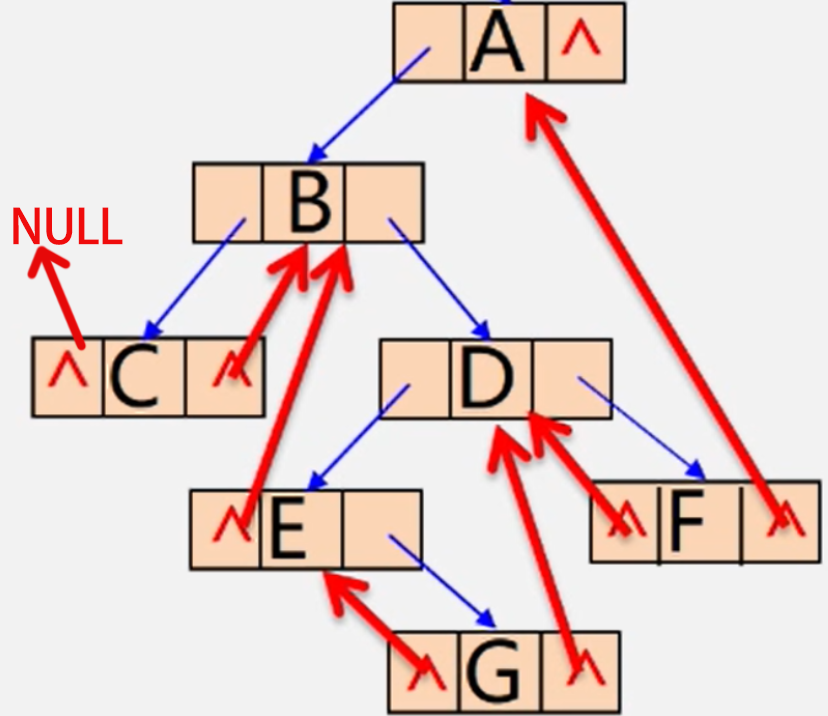
线索化步骤
- 先写出遍历顺序。
- 按照遍历顺序为节点添加左右指针。
平衡二叉树
定义:保持有序的情况下,任意节点的左右子树深度相差不超过 1。
图
- 有向图:节点之间有方向指的是有向图。
- 无向图:节点之间没有方向表示指的是无向图。
- 完全图
- 在无向图中,每对顶点都有一条边,称为完全图。
- 在有向图中,没对顶点之间都有两条边,称为完全图。
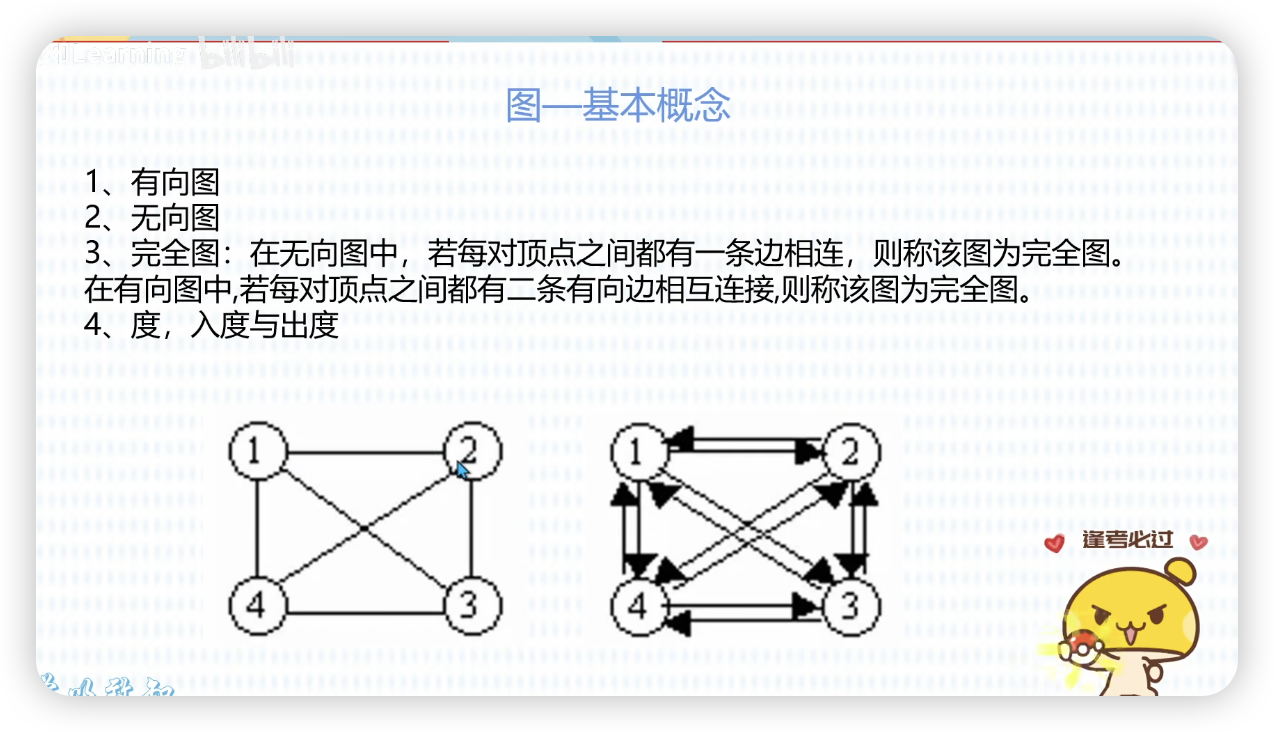
- 入度:指向某节点的边数量。
- 出度:某节点指向别的节点的数量。
邻接矩阵
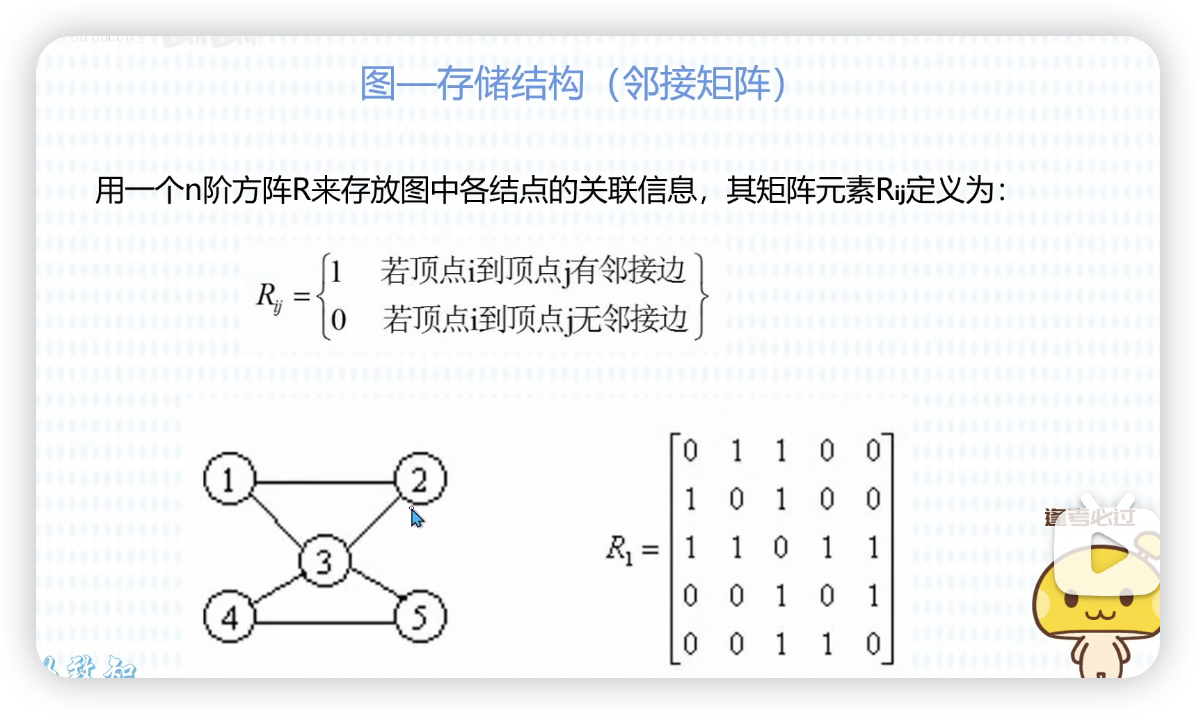
比如 5个元素,对应一个 5x5 的矩阵。
0 1 1 0 0
1 0 1 0 0
1 1 0 1 10 0 1 0 10 0 1 1 0邻接表
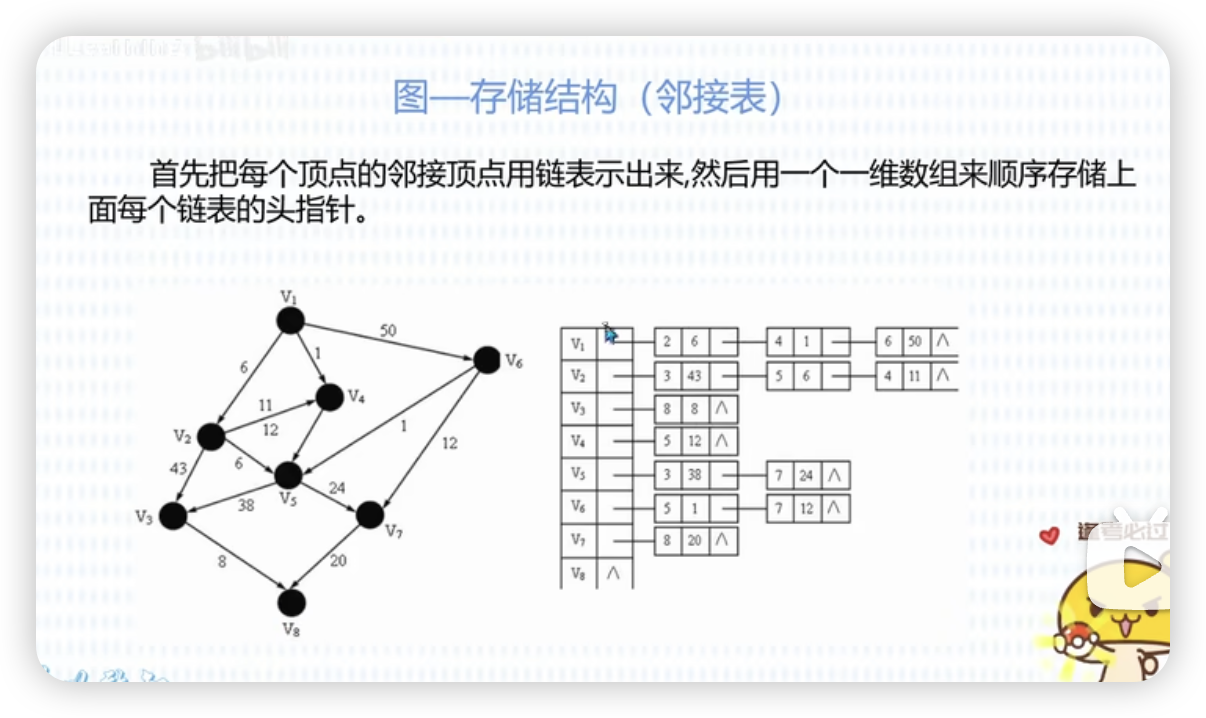
节点的出指向以链表的形式展示。
比如 v1 分别指向 v2、v4、v6 展示为 v1→v2→v4→v6。
图的遍历
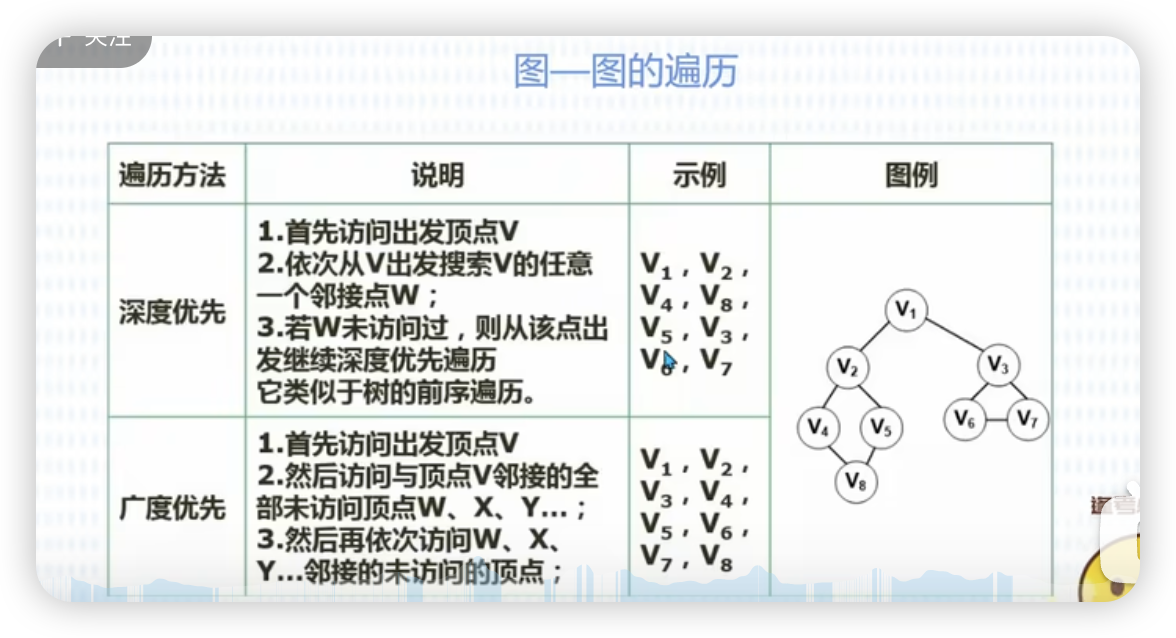
深度优先
优先向下遍历
广度优先
优先遍历左右子树
拓扑排序
AOV网,表示图的活动顺序。
有的节点需要等待前序活动结束。排序时需要注意前序结束。
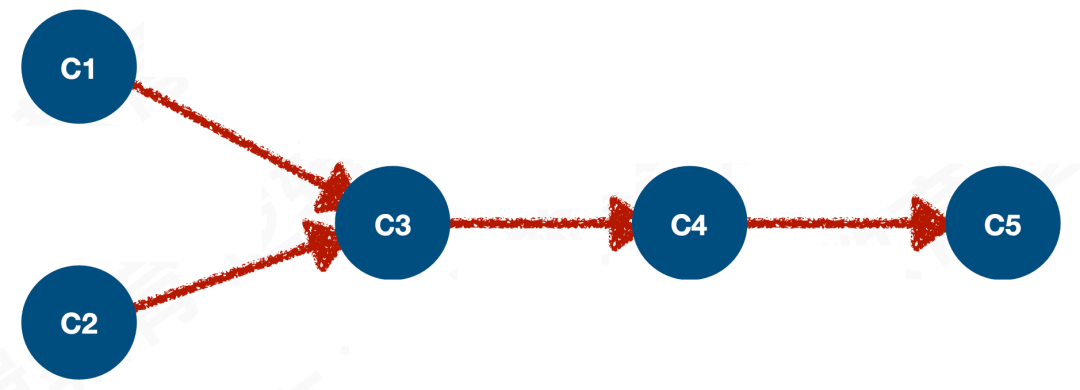
比如 C1、C2、C3、C4、C5 这个图。
AOV图的话,C3需要等待C1和C2完成。
所以排序可以是1、2、3、4、5 或 2、1、3、4、5。
拓扑排序不止是一种方式。
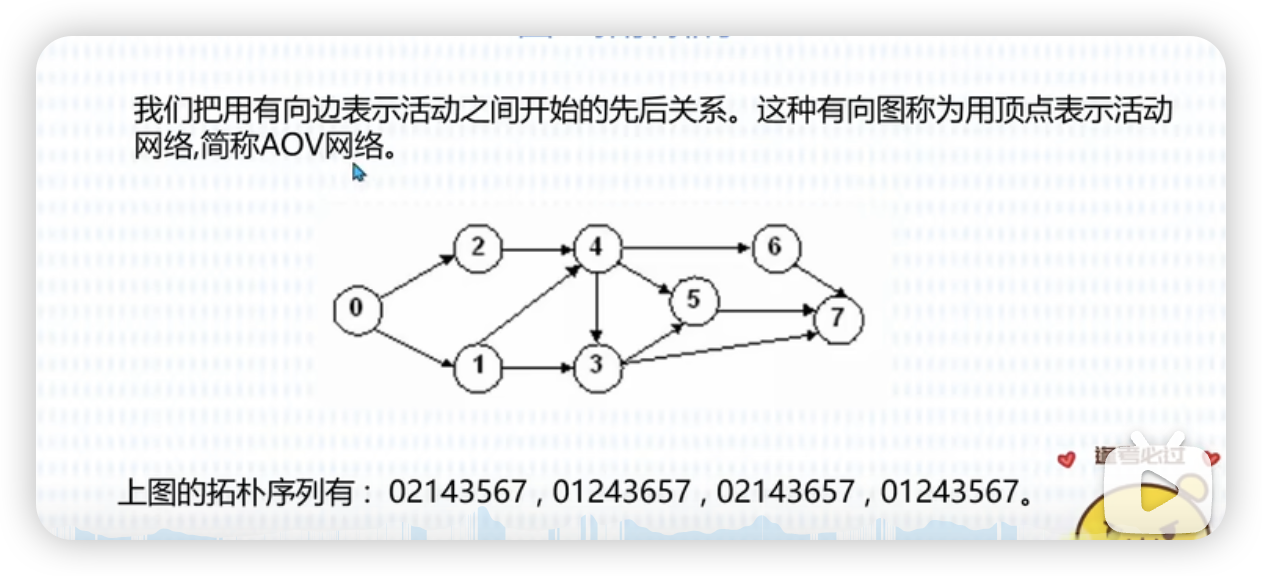
在工程的实施过程中,有些活动的开始是以它所有前序活动的结束为先决条件的,必须在其他有关活动完成之后才能开始;有些活动没有先决条件,可以安排在任意时间开始。AOV网就是一种可以形象地反映出整个工程中各个活动之间的先后关系的有向图。
AOV,Activity On Vertex Network,即顶点活动网。一个工程常常会被分为多个小的子工程,这些子工程被称为活动,在有向图中,若以顶点表示活动,有向边(也可以称为弧)表示活动之间的先后关系,这样的图简称为AOV网。
最小生成树
生成树:无向图中,一个连通图的最小连通子图称作该图的生成树(不能带环,保持连通,但边要尽可能的少)。
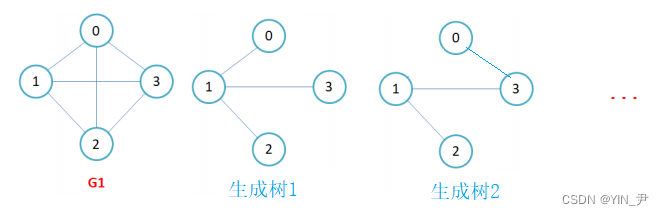
这里的最小生成树,指的是路径带权最小。
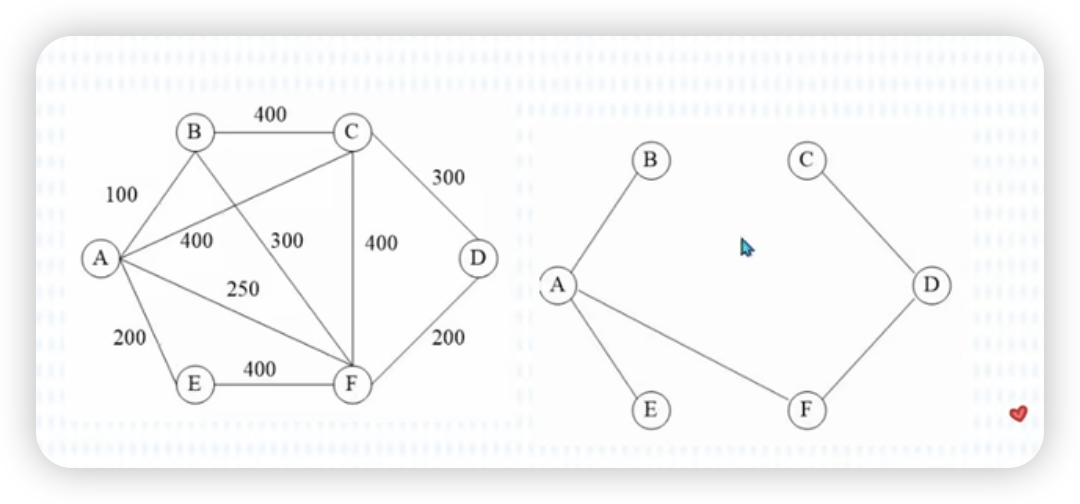
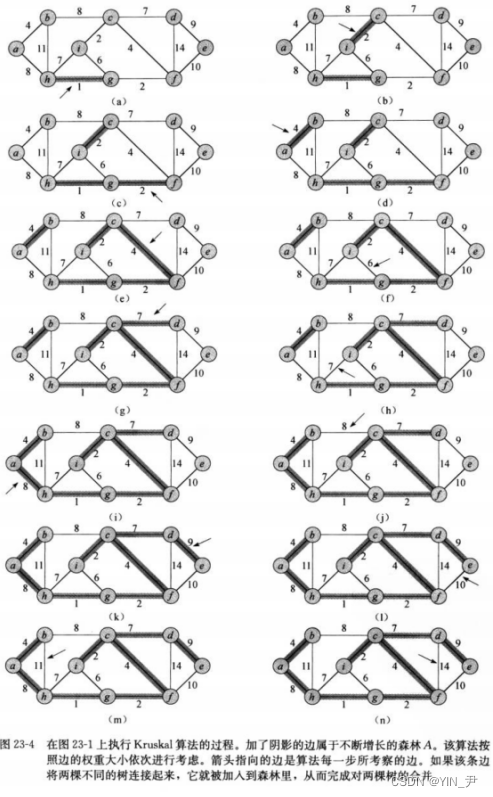
Kruskal算法-克鲁斯卡尔算法
每次**从图中还未被选到的所有的边里面选出权值最小且不会构成环的边,**构成的生成树就是该图对应的最小生成树。
核心是按照权重选最小边。
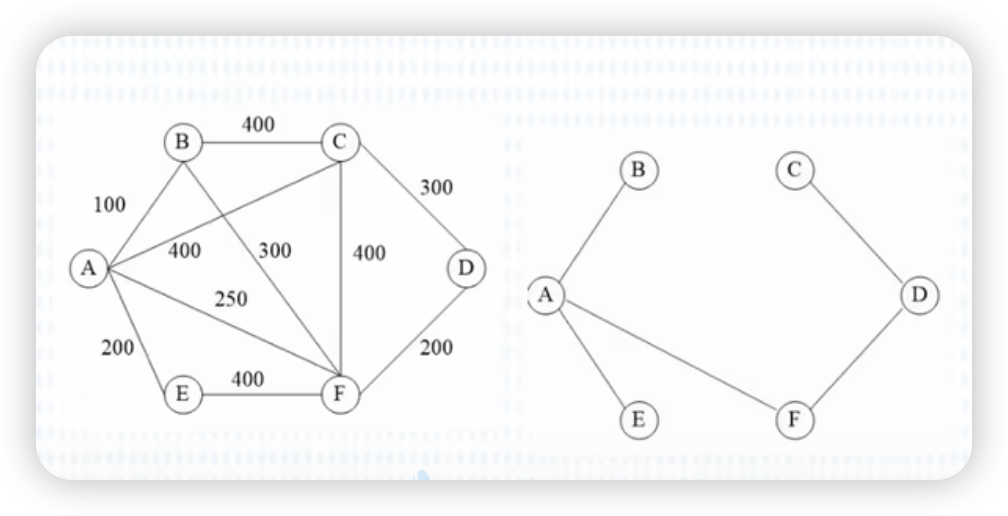
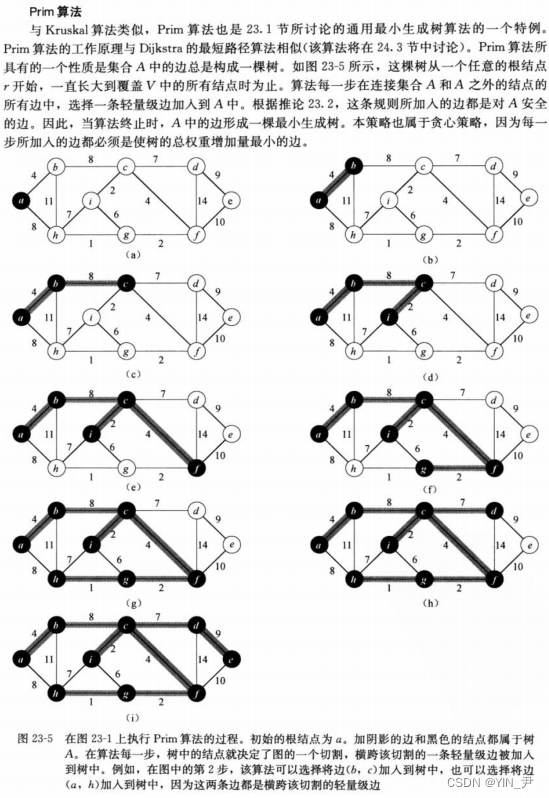
Prim算法-普鲁姆算法
任选一个节点,然后将节点分为两部分。一部分是已选择的节点,另一部分是未选择的节点。
然后以选择节点为根,从未选择节点中挑选出权重最小的边。
核心是按照权重选择最小节点。