二叉树
推荐一个练习数据结构的网站
二叉树的遍历(重要)
以图示二叉树为例。
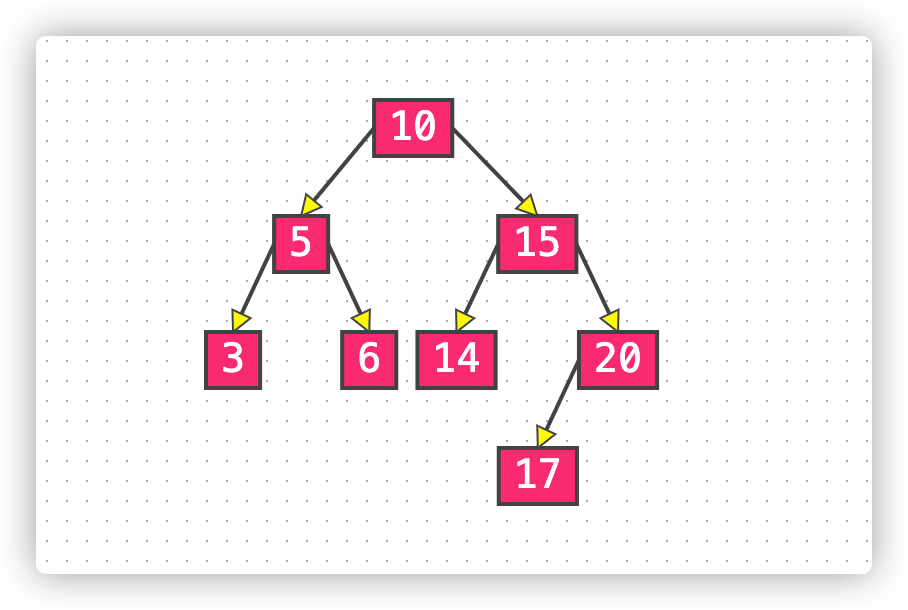
中序遍历
简化为每个树,都是左中右即可。
中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
左子树 → 根节点 → 右子树
图示二叉树中序遍历结果为:3、5、6、10、14、15、17、20;
参考代码:Java实现中序遍历
前序遍历
前序遍历(VLR), [1] 是二叉树遍历的一种,也叫做先根遍历、先序遍历、前序周游,可记做根左右。前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。
根节点 -> 左子树 -> 右子树
图示二叉树前序遍历结果为:10、5、3、6、15、14、20、17;
后序遍历
后序遍历(LRD)是二叉树遍历的一种,也叫做后根遍历、后序周游,可记做左右根。后序遍历有递归算法和非递归算法两种。在二叉树中,先左后右再根,即首先遍历左子树,然后遍历右子树,最后访问根结点。
左子树 -> 右子树 -> 根节点
图示二叉树后序遍历结果为:3、6、5、14、17、20、15、10;
层序遍历
二叉树的层次遍历 ,顾名思义就是指从二叉树的第一层(根节点)开始,从上至下逐层遍历,在同一层中,则按照从左到右的顺序对节点逐个访问。在逐层遍历过程中,按从顶层到底层的次序访问树中元素,在同一层中,从左到右进行访问。
图示二叉树层序遍历结果为:10、5、15、3、6、14、20、17;
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树。
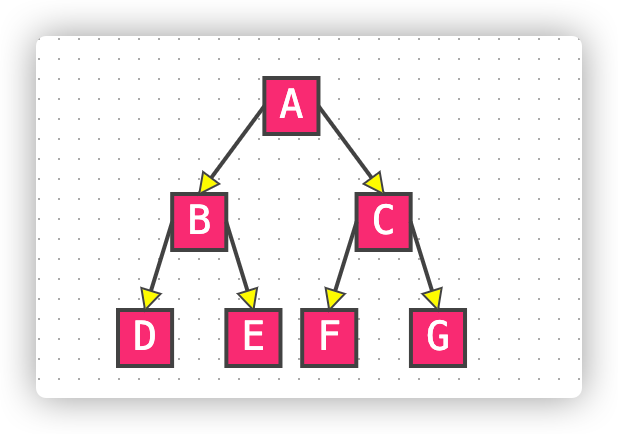
完全二叉树
一棵深度为k的有n个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号,如果编号为i(1≤i≤n)的结点与满二叉树中编号为i的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树
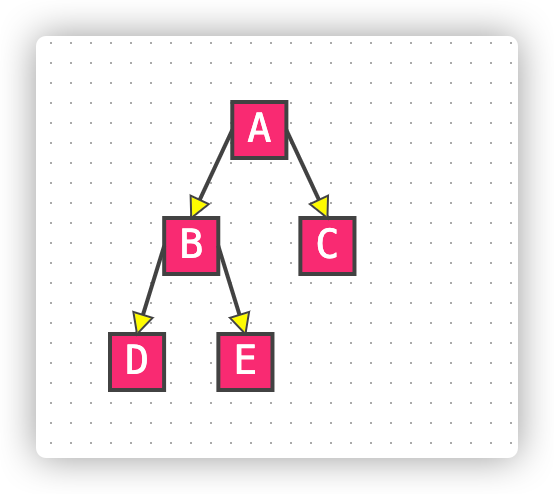
二叉查找树(重要)
特点
- 任何节点的左节点都小于该节点。
- 任何节点的右节点都大于该节点。
- 查找速率高于链表。
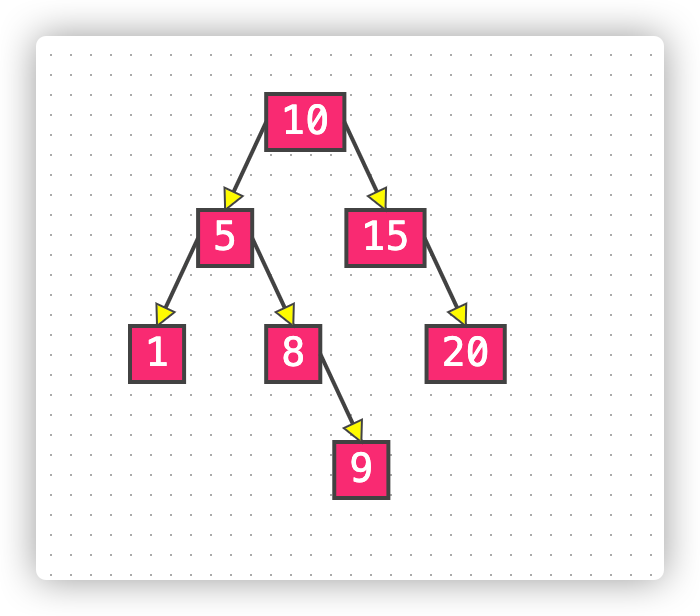
缺点
二叉查找树在特定情况下会退化成链表,若插入的元素是连续的,则会形成一个链表。
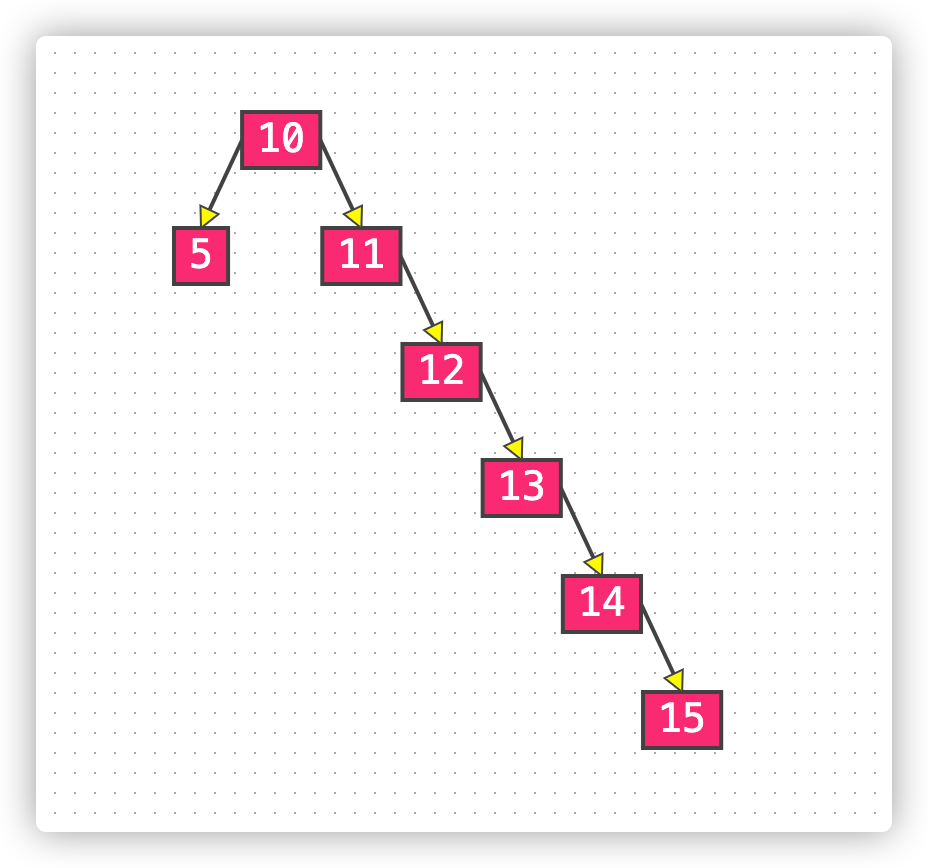
平衡二叉树(重要)
平衡二叉树又称 AVL Tree ,平衡二叉树是自平衡的,保证任何节点左右子树的高度差不能大于1。
优化了二叉查找树退化成链表的现象。
定义:任意节点的左右子树深度不能超过 1。
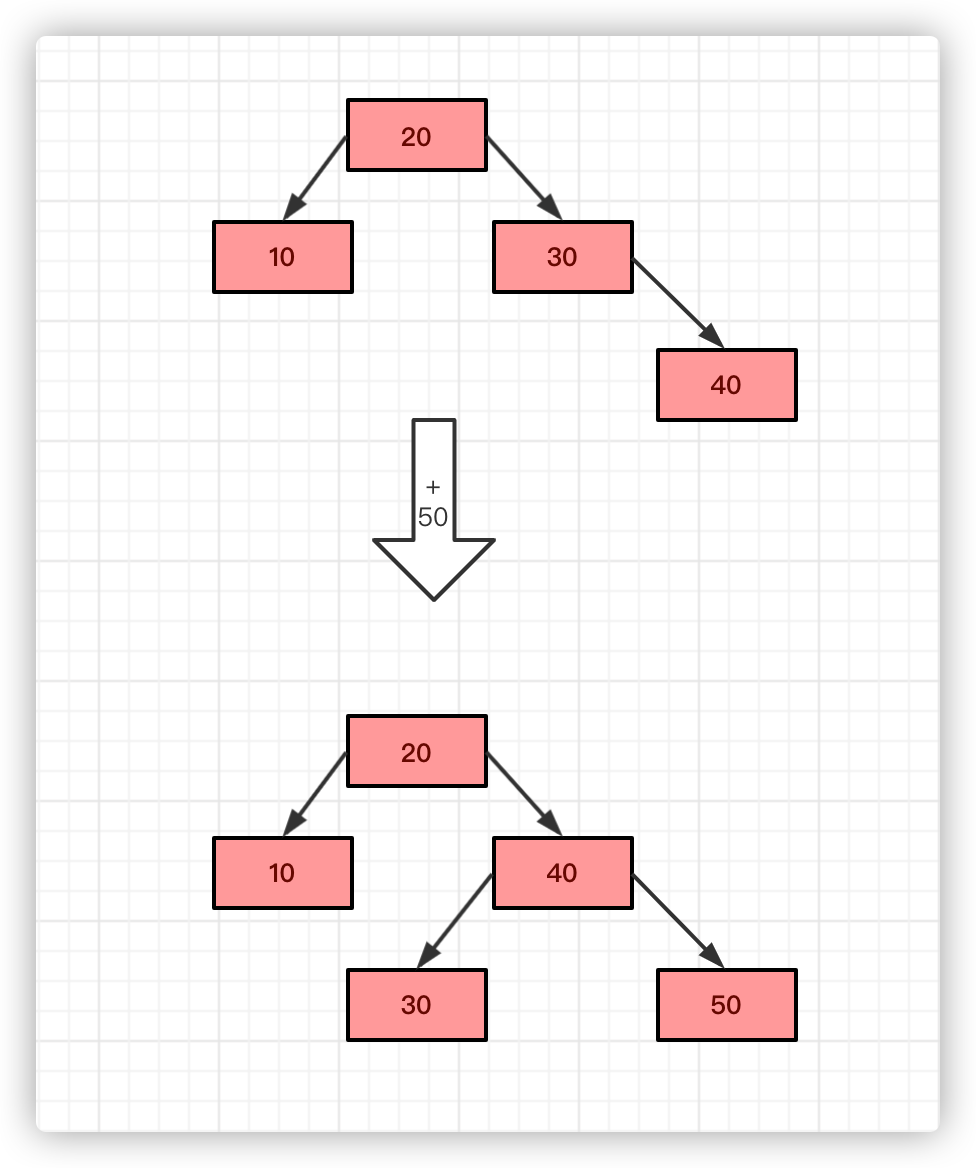
二叉树的刷题框架。
二叉树基本和递归有关,不要跳进递归的细节。
- 明确根节点要做什么
- 套用前序/中序/后序的遍历框架。