动态规划
动态规划重要特性
动态规划的核心问题是穷举,因为要求最值,要把所有可行答案找出来,找最值。但是穷举的过程中,会存在【重叠子问题】。
重叠子问题
在求解的过程中,存在重复的子问题,若是重复解决这些子问题,存在效率低下的问题。
而解决重叠子问题,可以使用【备忘录】或者【DP table】方法来解决。
备忘录
备忘录的思想就是将已经解决的子问题结果记录在备忘录中(可以是数组等数据结构)。
比如将子问题计算结果存到备忘录(数组),计算下个子问题时,先判断备忘录中是否存在计算结果。
DP table
使用 DP table 保存每个子问题的结果,自下向上推算结果。
斐波那契数列的解决过程体现了重叠子问题的解决思路,可以参考斐波那契数列的实现思路。
最优子结构
把原问题分解成若干个规模更小的子问题。
- 子问题独立。
- 原问题可以组合子问题的最优解。
重叠子问题-斐波那契数列
斐波那契数列中,体现了重叠子问题的特性。
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。
1. 暴力递归
根据斐波那契数列的表达式:F[n]=F[n-1]+F[n-2](n>=2,F[0]=0,F[1]=1),可以使用暴力递归从 n 开始由上向下计算 F[n] 的结果。
- 对于递归问题,一定要画出递归树。
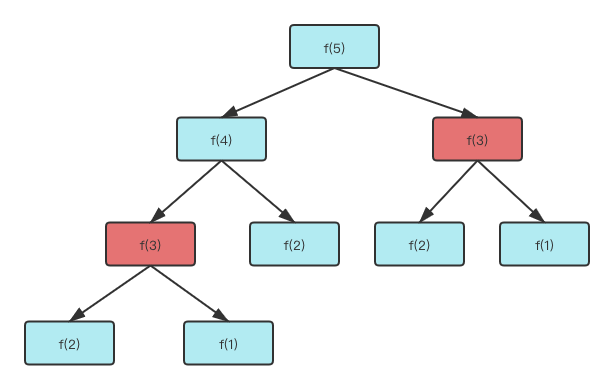
递归的时间复杂度
递归的子问题个数 * 子问题解决时间。
暴力递归求斐波那契数的子问题个数是指数倍的,即 2^n,而每个子问题的计算实际上就是个加法运算,解决时间的复杂度为
o(1)。所以 暴力递归求斐波那契数的时间复杂度是 o(2^n)。
实现代码
public int fibForce(int n) {
if (n == 0) {
return 0;
}
if (n == 1 || n == 2) {
return 1;
}
//递归计算前两个数的和
return fibForce(n - 1) + fibForce(n - 2);
}暴力递归的缺陷
通过递归树可以发现,计算
f(3)等子问题的时候发生了重复计算的问题,即发生了【重叠子问题】的现象。这也是暴力递归效率低下的原因,可以通过【备忘录】和【DP-table】来优化。
2. 带备忘录的递归
在明确了子问题会发生重复计算的问题情况下,可以使用数组或者哈希表等创建一个备忘录,来保存子问题的计算结果。
/**
* 使用备忘录
* 从递归树自上向下计算
*/
public int fibBackup(int n) {
//备忘录【保存已计算的结果】
int[] nums = new int[n + 1];
return helper(nums, n);
}
private int helper(int[] nums, int n) {
if (n == 0 || n == 1) {
return n;
}
//判断数组【备忘录】是否已存在数据
if (nums[n] != 0) {
return nums[n];
}
nums[n] = helper(nums, n - 1) + helper(nums, n - 2);
return nums[n];
}对应的递归树如下图,对比下可以发现子问题 f(3) 只计算了一次。
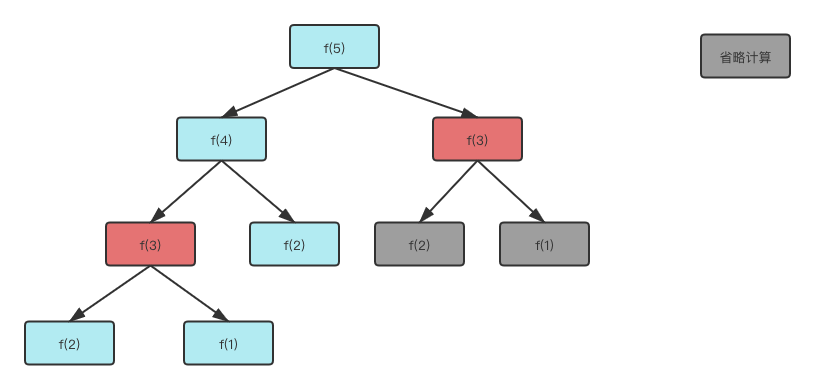
递归的时间复杂度是 递归的子问题个数 * 子问题解决时间。
使用了备忘录之后,由于不存在重复计算,每个子问题只计算一次,所以递归的子问题个数变为了 n 个。而解决时间是不变的为 o(1)。
所以 带备忘录的递归求斐波那契数的时间复杂度是 o(n)。
3. DP-table
不论是暴力递归还是带备忘录的递归,本质上都是从 F(n) 开始由上向下计算。由于我们已知最小的 F(0) 和 F(1) 的结果值,根据 F(0) 和 F(1) 可求出 F(2)的结果,然后将计算的结果存到类似备忘录的数组或哈希表中(称为 DP-table)。根据表达式可以实现由下往上计算,最终可得出 F(n) 的结果。
本质上由上向下和由下往上的效率是一致的。
public int fib(int n) {
//DP-table
if (n == 0 || n == 1) {
return n;
}
//设置初始值
int[] nums = new int[n + 1];
nums[1] = 1;
for (int i = 2; i <= n; i++) {
//保存子问题结果到DP-table
nums[i] = nums[i - 1] + nums[i - 2];
}
return nums[n];
}在DP-table 的使用过程,可以发现其实使用到 DP-table 的数据只是最近两个子问题的结果,通过优化可以节省 DP-table 的空间。
public int fibOptimization(int n) {
//n-2 子问题结果
int pre=0;
//n-1 子问题结果
int curr=1;
//n 子问题结果
int sum=0;
if (n == 0 || n == 1) {
return n;
}
for (int i = 2; i <= n; i++) {
sum = pre+curr;
pre=curr;
curr=sum;
}
return sum;
}